matplotlibは、Pythonでグラフを作成する際に便利なライブラリです。
ここでは、matplotlibを用いて、Pythonで平面的な分布図を作成する方法について解説したいと思います。
作成する図は、下のようなものです。
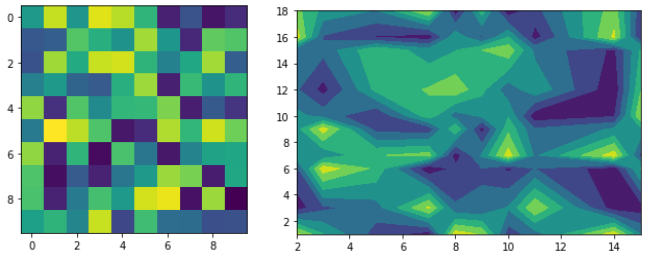
1.座標を持たないマトリックスデータの場合(imshow)
まずは、座標を持たないマトリックスデータの場合の図化についてです。
マトリックスデータとは、下のように行列の状態になっているデータです。(下の例は6行4列のマトリックスデータ)
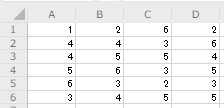
このようなデータの場合、簡単に図化することができます。
では、まず下のコードを実行してみてください。
import numpy as np import matplotlib.pyplot as plt img = np.random.rand(10, 10) plt.imshow(img) plt.show()
すると、下のような図ができたと思います。(imgはランダムで与えているため、模様は実行するたびに変わります。)
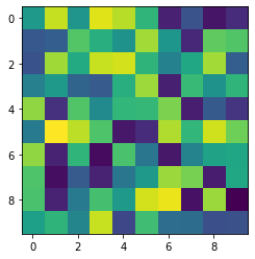
では、詳しく解説していきます。
まず1行目と2行目は、必要なライブラリをインポートしているだけです。
次に3行目の
img = np.random.rand(10, 10)
では、「img」という変数に10×10のランダムな数字のマトリックスを入れる、という操作です。
ここまでが準備段階ですね。
そして、肝心のマトリックスデータのグラフ化ですが、
plt.imshow(img)
のみで出来てしまします!
このように、マトリックスデータの図化は基本的に「plt.imshow(マトリックスデータ)」で、簡単に図化することができます!
ただし、データが全て等間隔で、行列のデータの間隔も同じになるため、使える場面は限られます。
また、「imshow」を使う場合、隣の値との補完などはなく、上の平面分布のようにきれいな四角で色が塗られます。
- マトリックスデータの図化は「plt.imshow(マトリックスデータ)」で、簡単に図化できる
- 「imshow」では、データが全て等間隔で、行列のデータの間隔も同じになる
- 「imshow」を使う場合、隣の値との補完などはなく、きれいな四角で色が塗られる
2.座標を持つマトリックスデータの場合(contourf)
次に、データが座標を持つ場合、すなわち(x,y,z)で表すことのできるデータの場合の図化について解説したいと思います。
この場合は、「contourf」というものを使います。
データ形のイメージは、下のようにマトリックスデータに座標がある場合と考えてください。
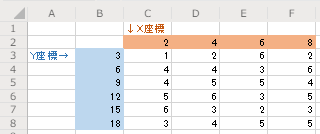
※上の場合、x座標の間隔は2、y座標の間隔は3になっていますが、座標の間隔は一定でなくても構いません。
では、こういった座標を持つマトリックスデータの図化を行っていきます。
下のコードを実行してください。
import numpy as np import matplotlib.pyplot as plt img = np.random.rand(10, 10) x = np.array([2,3,5,7,8,9,10,11,14,15]) y = np.array([1,3,6,7,9,10,12,15,16,18]) xx, yy = np.meshgrid(x, y) plt.contourf(xx, yy, img) plt.show()
すると、下のような図ができたと思います。
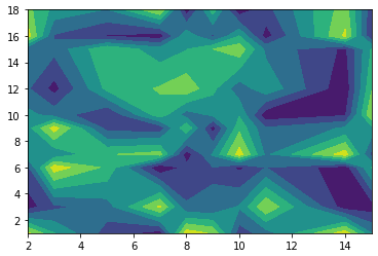
では、詳しく解説していきます。
「imshow」を用いた時との違いは、4~7行目の
x = np.array([2,3,5,7,8,9,10,11,14,15]) y = np.array([1,3,6,7,9,10,12,15,16,18]) xx, yy = np.meshgrid(x, y) plt.contourf(xx, yy, img)
です。この中で、
x = np.array([2,3,5,7,8,9,10,11,14,15]) y = np.array([1,3,6,7,9,10,12,15,16,18])
では、それぞれX座標とY座標をそれぞれ指定しています。
(今回は10×10のマトリックスデータのため、X座標とY座標をそれぞれ10ずつ用意)
次が座標を持つマトリックスデータを図化する上で重要で、また分かりにくいポイントなのですが、
xx, yy = np.meshgrid(x, y)
では、x座標とy座標をそれぞれグリッド化(マトリックス化)しています。
といっても分からないと思うので、下の図を見てください。
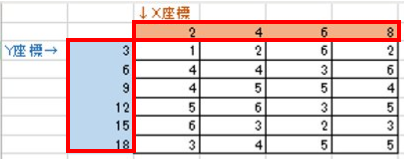
上の図は、6×4のマトリックスデータにxy座標が与えられたものです。
例えば、x=4、y=12といえば、「6」となります。
これをmatplotlibで図化する場合は、x座標とy座標もそれぞれ6×4のマトリックスデータにする必要があり、その操作を行っています。
np.meshgrid()を用いたx座標とy座標、それぞれのマトリックスデータ(xx、yy)の作成イメージは、下のようなものです。
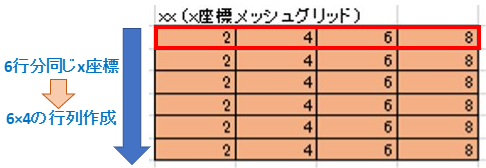
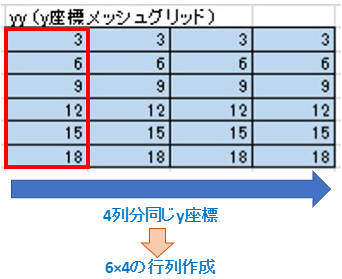
このxxとyyを重ねると、6×4の座標のマトリックスができますね。
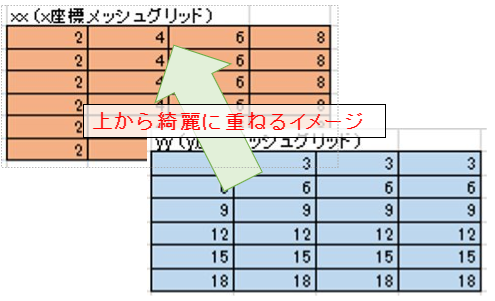
こうしてx座標とy座標のグリッドデータが作成出来たら、後は「plt.contourf(x座標グリッド, y座標グリッド, マトリックスデータ)」で、分布図を作成できます!
また、「contourf」ではデータの間が近くのデータで補完されるため、「imshow」と違い、滑らかな分布になります。
また、「contourf」でも、座標を持たないマトリックスデータに疑似的に座標を与えることで図化できるため、「imshow」に比べ応用が利きます。
ですので、ぜひ「contourf」で図化できるようになってください。
- 座標を持つマトリックスデータの図化には「contourf」を使う
- 「meshgrid」を用いて、x座標とy座標をそれぞれグリッド化(マトリックス化)して図化する
- 「contourf」ではデータの間が近くのデータで補完されるため、滑らかな分布になる
3.座標を持つ非マトリックスデータの場合
最後に、座標を持つ非マトリックスデータの図化について解説したいと思います。
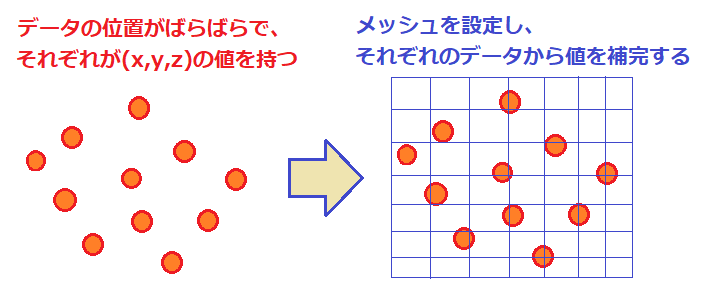
非マトリックスデータとは、下のイメージのように、値がばらばらの位置にあるようなデータです。

この場合も、「座標を持つマトリックスデータ」の時と同様に、「contourf」を使います。
図化の過程としては、下の図のようにメッシュを設定し、ばらばらのデータからメッシュの値を補完して図化する(マトリックス化)、といった処理を行います。
では、実際に図化を行ってみましょう。
下のコードを実行してください。
import numpy as np import matplotlib.pyplot as plt from scipy.interpolate import griddata x = np.array([0,3,6,4,8]) y = np.array([1,6,10,7,8]) z = np.random.rand(5) xmin = x.min() xmax = x.max() ymin = y.min() ymax = y.max() msize = 1 ax = np.arange(xmin,xmax,msize) ay = np.arange(ymin,ymax,msize) xx, yy = np.meshgrid(ax, ay) nz = griddata((x, y), z, (xx, yy)) plt.contourf(xx, yy, nz) plt.show()
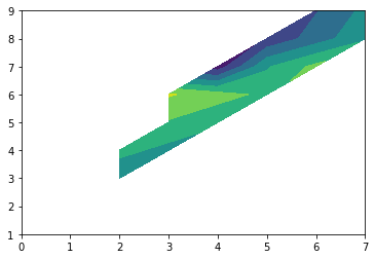
すると、下のような図ができたと思います。
では詳しく解説していきます。
まず、4~6行目で(0,1)、(3,6)、(6,10)、(4,7)、(8,8)という5つの座標のデータを作成しています。(zのデータはランダムです。)
x = np.array([0,3,6,4,8]) y = np.array([1,6,10,7,8]) z = np.random.rand(5)
次に、7~11行目で設定するメッシュ範囲の最小値、最大値とメッシュサイズを指定しています。
(今回はメッシュ範囲をそれぞれx、yの最大値、最小値で設定しています。)
xmin = x.min() xmax = x.max() ymin = y.min() ymax = y.max() msize = 1
そして、12~14行目で、上のコードで設定したメッシュ範囲とメッシュサイズのメッシュを作成しています。
ax = np.arange(xmin,xmax,msize) ay = np.arange(ymin,ymax,msize) xx, yy = np.meshgrid(ax, ay)
そして、次の部分がポイントです!
15行目の下のコードでは、「もともとのデータ(x, y)から、メッシュデータ(xx, yy)へzの値を補完する」という操作を行っています。
nz = griddata((x, y), z, (xx, yy))
イメージは、最初に説明した下の図の操作です。

これで、非マトリックスデータの図化をすることができました!
ただし、完成した図を見て、「余白が多いな?」と感じた方もいると思います。
これは、ランダムに配置したデータが、設定したメッシュを補完できる場所にデータが無いため起こっています。
イメージ図で説明すると、以下のような形です。
メッシュの値を補完するためには、そのメッシュを囲うようにデータが無ければなりません。
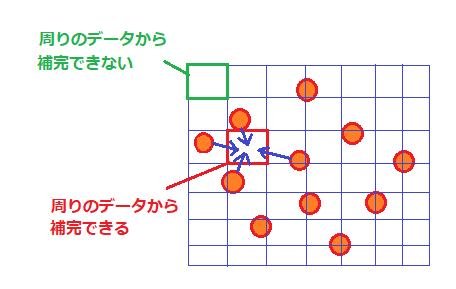
実際に、メッシュとして補完した「nz」をspyderで確認すると、下のように「nan」となり、値が保管されていない場所があることが分かります。
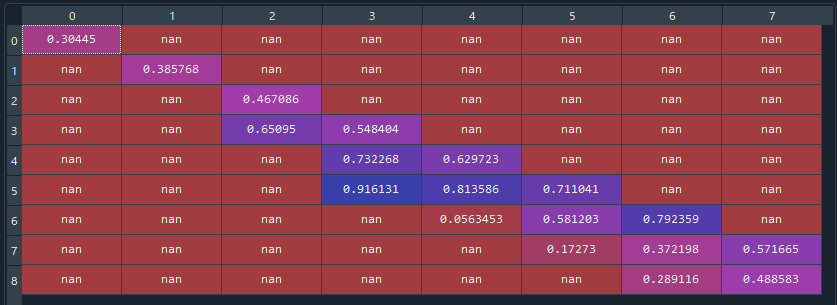
ちなみに、「spyder」での変数の見方などは、「Spyderの基本と便利な使い方」で解説していますので、気になった方はそちらもご覧ください。
また、きれいなグラフを作りたい場合はデータの範囲とデータ数を増やし、図化に使用するメッシュの範囲を少し小さめに設定すると、すべてのメッシュを補完することができるのできれいに図化することができます。
import numpy as np import matplotlib.pyplot as plt from scipy.interpolate import griddata x = np.random.randint(0,100,100) y = np.random.randint(0,100,100) z = np.random.rand(100) xmin = x.min()+10 xmax = x.max()-10 ymin = y.min()+10 ymax = y.max()-10 msize = 2 ax = np.arange(xmin,xmax,msize) ay = np.arange(ymin,ymax,msize) xx, yy = np.meshgrid(ax, ay) nz = griddata((x, y), z, (xx, yy)) plt.contourf(xx, yy, nz) plt.show()
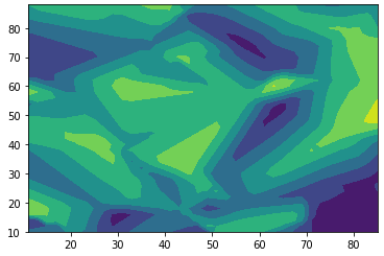
上の図は、xとyをそれぞれ0~100の範囲でランダムに100個の座標を設定し、その後その範囲からそれぞれ10だけ狭い範囲でメッシュを作成して図化したものです。
これで、非マトリックスデータの場合でも図化することができました!
- 非マトリックスデータの場合「griddata」を用いてデータをメッシュ化して図化する
- 非マトリックスデータでも「contourf」を用いて図化する
4.まとめ
今回は、「matplotlib」を用いた平面分布図の作成方法について解説しました。
私自身、平面分布図を作図する機会があったのですが、非マトリックスデータの作図について学べるサイトが無く、苦労しました。
当時の私と同じような悩みを持った方が、このサイトでその悩みを解決できれば幸いです。
また、凡例や色合いの設定についての解説は「2次元平面分布図における範囲外の凡例や色合いの設定」で解説していますので、そちらをご覧ください。
なお、このサイトでは初心者の方向けに「Python初心者入門講座」という講座を作成していますので、気になった方はそちらもご覧ください。










コメント